Understand the foundations of probability and its relationship to statistics and data science. We’ll learn what it means to calculate a probability, independent and dependent outcomes, and conditional events. We’ll study discrete and continuous random variables and see how this fits with data collection. We’ll end the course with Gaussian (normal) random variables and the Central Limit Theorem and understand its fundamental importance for all of statistics and data science.


Probability Theory: Foundation for Data Science
This course is part of Data Science Foundations: Statistical Inference Specialization
Taught in English
Some content may not be translated


Instructors: Anne Dougherty
22,438 already enrolled
Included with 
Course
(152 reviews)
90%
Recommended experience
What you'll learn
Explain why probability is important to statistics and data science.
See the relationship between conditional and independent events in a statistical experiment.
Calculate the expectation and variance of several random variables and develop some intuition.
Skills you'll gain
Details to know

Add to your LinkedIn profile
6 quizzes
Course
(152 reviews)
90%
Recommended experience
See how employees at top companies are mastering in-demand skills

Build your subject-matter expertise
- Learn new concepts from industry experts
- Gain a foundational understanding of a subject or tool
- Develop job-relevant skills with hands-on projects
- Earn a shareable career certificate


Earn a career certificate
Add this credential to your LinkedIn profile, resume, or CV
Share it on social media and in your performance review

There are 7 modules in this course
Welcome to the course! This module contains logistical information to get you started!
What's included
6 readings1 app item1 discussion prompt1 ungraded lab
Understand the foundation of probability and its relationship to statistics and data science. We’ll learn what it means to calculate a probability, independent and dependent outcomes, and conditional events. We’ll study discrete and continuous random variables and see how this fits with data collection. We’ll end the course with Gaussian (normal) random variables and the Central Limit Theorem and understand it’s fundamental importance for all of statistics and data science.
What's included
3 videos3 readings1 quiz1 programming assignment1 ungraded lab
The notion of “conditional probability” is a very useful concept from Probability Theory and in this module we introduce the idea of “conditioning” and Bayes’ Formula. The fundamental concept of “independent event” then naturally arises from the notion of conditioning. Conditional and independent events are fundamental concepts in understanding statistical results.
What's included
2 videos2 readings1 quiz1 programming assignment1 ungraded lab
The concept of a “random variable” (r.v.) is fundamental and often used in statistics. In this module we’ll study various named discrete random variables. We’ll learn some of their properties and why they are important. We’ll also calculate the expectation and variance for these random variables.
What's included
4 videos2 readings1 quiz1 programming assignment1 ungraded lab
In this module, we’ll extend our definition of random variables to include continuous random variables. The concepts in this unit are crucial since a substantial portion of statistics deals with the analysis of continuous random variables. We’ll begin with uniform and exponential random variables and then study Gaussian, or normal, random variables.
What's included
4 videos3 readings1 quiz1 programming assignment1 ungraded lab
The power of statistics lies in being able to study the outcomes and effects of multiple random variables (i.e. sometimes referred to as “data”). Thus, in this module, we’ll learn about the concept of “joint distribution” which allows us to generalize probability theory to the multivariate case.
What's included
3 videos2 readings1 quiz1 programming assignment
The Central Limit Theorem (CLT) is a crucial result used in the analysis of data. In this module, we’ll introduce the CLT and it’s applications such as characterizing the distribution of the mean of a large data set. This will set the stage for the next course.
What's included
2 videos3 readings1 quiz1 programming assignment1 ungraded lab
Instructors


Offered by
Recommended if you're interested in Probability and Statistics
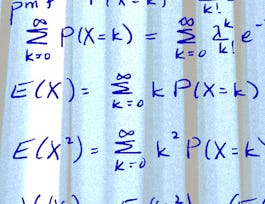
University of Colorado Boulder
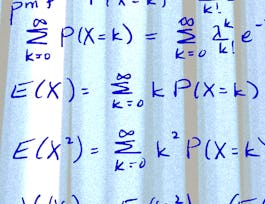
University of Colorado Boulder
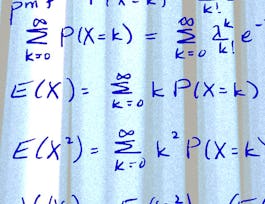
University of Colorado Boulder
Coursera Project Network
Get a head start on your degree
This course is part of the following degree programs offered by University of Colorado Boulder. If you are admitted and enroll, your coursework can count toward your degree learning and your progress can transfer with you.
Why people choose Coursera for their career




Learner reviews
Showing 3 of 152
152 reviews
- 5 stars
75.16%
- 4 stars
12.41%
- 3 stars
3.26%
- 2 stars
2.61%
- 1 star
6.53%
New to Probability and Statistics? Start here.

Open new doors with Coursera Plus
Unlimited access to 7,000+ world-class courses, hands-on projects, and job-ready certificate programs - all included in your subscription
Advance your career with an online degree
Earn a degree from world-class universities - 100% online
Join over 3,400 global companies that choose Coursera for Business
Upskill your employees to excel in the digital economy
Frequently asked questions
Access to lectures and assignments depends on your type of enrollment. If you take a course in audit mode, you will be able to see most course materials for free. To access graded assignments and to earn a Certificate, you will need to purchase the Certificate experience, during or after your audit. If you don't see the audit option:
The course may not offer an audit option. You can try a Free Trial instead, or apply for Financial Aid.
The course may offer 'Full Course, No Certificate' instead. This option lets you see all course materials, submit required assessments, and get a final grade. This also means that you will not be able to purchase a Certificate experience.
When you enroll in the course, you get access to all of the courses in the Specialization, and you earn a certificate when you complete the work. Your electronic Certificate will be added to your Accomplishments page - from there, you can print your Certificate or add it to your LinkedIn profile. If you only want to read and view the course content, you can audit the course for free.
If you subscribed, you get a 7-day free trial during which you can cancel at no penalty. After that, we don’t give refunds, but you can cancel your subscription at any time. See our full refund policy.